外观
Skip to content 查看源代码:
查看源代码:
even-picture-solution.md
---
title: Even Picture 的 n+O(√n) 构造
createTime: 2024/10/07
categories:
- IT
tags:
- OI
- maths
---
本蒟蒻的第一篇题解,求过。
## 成为最优构造的必要条件:
AC [CF1368C Even Picture(加强加强加强加强版)](https://www.luogu.com.cn/problem/U487982)
## 大概是最优构造:
由于楼上同样是 $n+O(\sqrt{n})$ 的大佬没有贴代码,所以比较不了。

用不同颜色将其分成了九块。
左上角/右下角块只有一个点染色,中间块除对角线外染色,其余块按三角形染色。
### 推算
设每块大小为 $s \times s$,由小学奥数可得
$$S_\text{总}=4s^2+2s+2$$
$$S_\text{冗余}=8s$$
$$S_\text{有效}=4s^2-6s+2$$
由于 $S_\text{有效} \le n$,根据求根公式,令
$$s=\left\lfloor \frac{6+\sqrt{16n+4}}{8} \right\rfloor$$
假如 $n-S_\text{有效}$ 的剩余部分用形如
```
##
###
###
###
##
```
的尾巴接在原图形上面,则有
$$k=S_\text{总}+3(n-S_\text{有效})$$
稍加计算可得
$$n+4\sqrt{n} \le k \le n+12\sqrt{n}$$
对于 $n \le 500$ 有 $k \le 748.$
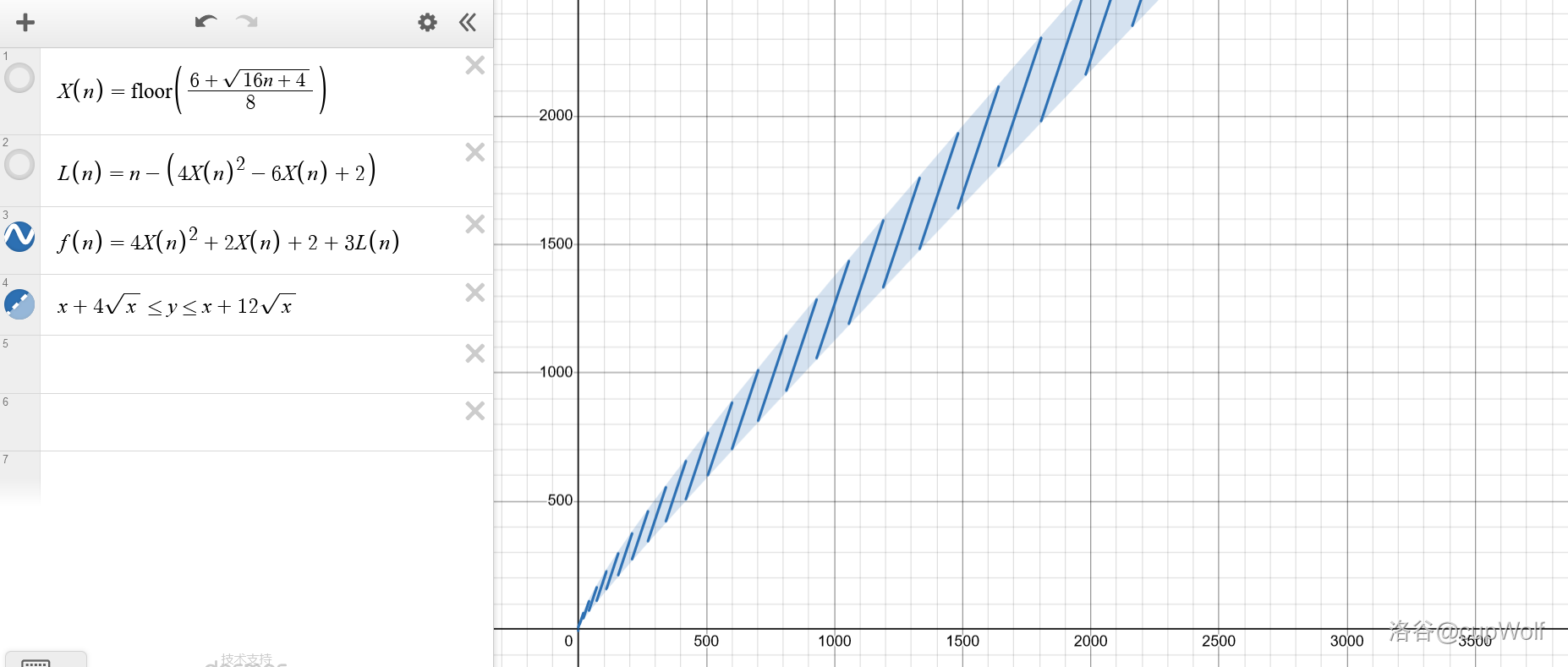
### 优化
如果小尾巴改成递归构造,则上界更新为 $\min\left(x+6\sqrt{x}+43,x+12\sqrt{x}\right)$ (纯靠手动调参拟合,一点都不紧)
对于 $n \le 1000$ 有 $k \le 1192.$
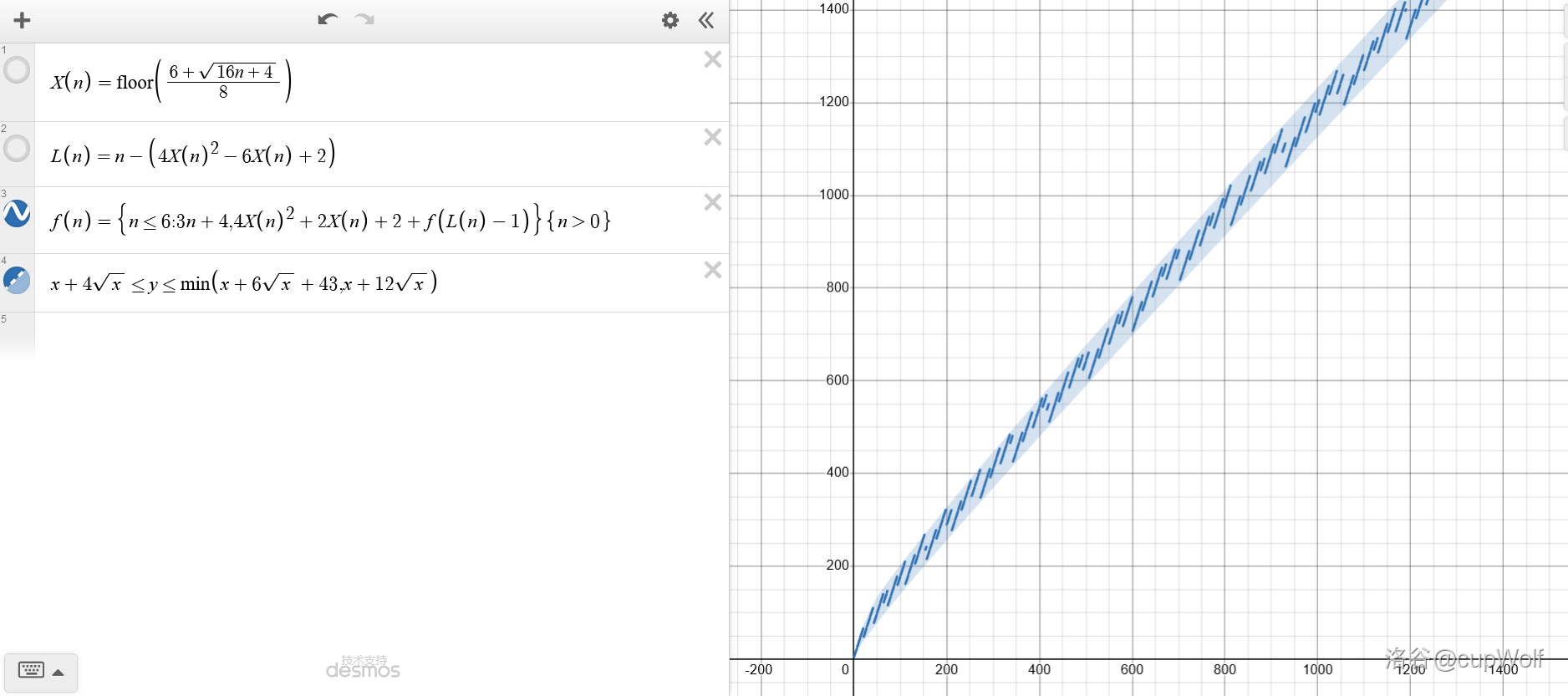
### 欣赏一下构造的图形
(在代码中调用 `canvas.debug()` 即可欣赏)
$n=500, k=640$
```
n=500, k=640
##
####
######
########
##########
############
##############
################
##################
####################
#######################
# #####################
### ###################
##### #################
####### ###############
######### #############
########### ###########
############# #########
############### ####### ##
################# ##### ####
################### ### ######
##################### # ########
#################################
#################### # #########
################## ### #######
################ ##### #####
############## ####### ###
############ ######### # ##
########## ###############
######## ######## # ###
###### ###### ### #
#### #### #####
## ## ##
```
## Code:
从普通版一直改到四次加强的屎山。
```cpp
#include <bits/stdc++.h>
using namespace std;
int n;
void small_main(){
printf("%d\n", 3*n+4);
printf(
"1 1\n"
"1 2\n"
"2 1\n"
"2 2\n"
);
for (int i=1; i<=n; i++){
printf(
"%d %d\n%d %d\n%d %d\n",
i+1, i+2,
i+2, i+1,
i+2, i+2
);
}
}
struct coord {
int x, y;
};
const int maxdebug=80;
char buf[90][90]; // debug only
inline int __flip(bool flip, int size, int x){
return flip ? (size+1-x) : x;
}
struct Canvas {
int xoff, yoff; // 每次画完之后把原点移动到特定位置,方便前后衔接
vector<coord> ans;
int cur_row = 1;
void draw(int x, int y){
ans.push_back({x+xoff, y+yoff});
}
void debug(){
memset(buf, ' ', sizeof buf);
for (int i=0; i<=maxdebug; i++){
buf[i][maxdebug+2] = '\n';
buf[i][maxdebug+3] = '\0';
}
for (coord &c: ans) {
buf[c.x][c.y] = '#';
}
for (int i=0; i<=maxdebug; i++){
cout << buf[i];
}
}
void output(){
printf("%d\n", ans.size());
for (coord &c: ans) {
printf("%d %d\n", c.x, c.y);
}
}
void draw_triangle(int size, int row, int col, bool xflip, bool yflip){
// xflip=yflip=0时
// ###
// ##
// #
// xflip 上下翻转,yflip 左右翻转
int x0 = row * size, y0 = col * size;
for (int i=1; i<=size; i++){
for (int j=1; i+j<=size+1; j++){
draw(x0 + __flip(xflip, size, i),
y0 + __flip(yflip, size, j));
}
}
}
void draw_dhyy(int size, int row, int col){
// 缺对角线的正方形
// ##
// # #
// ##
int x0 = row * size, y0 = col * size;
for (int i=1; i<=size; i++){
for (int j=1; j<=size; j++){
if (i != j){
draw(x0+i, y0+j);
}
}
}
}
} canvas;
int main(){
cin >> n;
if (n<=30){
small_main();
return 0;
}
bool flag = false;
// flag = not 是不是最左上角的
// 处理衔接用
while (n >= 7) {
if (flag){
n--;
}
int size = sqrt(16*n+4);
size = (size + 6) / 8;
// printf("size=%d\n", size);
if (!flag){
canvas.draw(size, size);
}
// 预留空间,1, 1 -> size, size
if (flag){
canvas.xoff -= size - 1;
canvas.yoff -= size - 1;
} else {
flag = true;
}
canvas.draw_triangle(size, 0, 1, 1, 1);
canvas.draw_triangle(size, 0, 2, 1, 0);
canvas.draw_triangle(size, 1, 0, 1, 1);
canvas.draw_dhyy(size, 1, 1);
canvas.draw_triangle(size, 1, 2, 0, 0);
canvas.draw_triangle(size, 2, 0, 0, 1);
canvas.draw_triangle(size, 2, 1, 0, 0);
canvas.draw(2*size+1, 2*size+1);
n -= 4*size*size - 6*size + 2;
// move 2*size+1, 2*size+1 -> 1, 1
canvas.xoff += 2*size;
canvas.yoff += 2*size;
}
for (int i=1; i<=n; i++){
canvas.draw(i+1, i);
canvas.draw(i, i+1);
canvas.draw(i+1, i+1);
}
// canvas.debug();
canvas.output();
return 0;
}
```