CF2136A. In the Dream

题意

给出比分，问是否存在一种得分序列满足一队不连续得分 $3$ 次。

稍加思考即可想出来。

被英文卡了，$c:d$ 是下半场之后的比分，不是下半场的得分。

AC Code

#include <bits/stdc++.h>
using namespace std;

inline bool isok(int a, int b) {
    return a>=0 && b>=0 && a<=b*2+2 && b<=a*2+2;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    
    int t;
    cin >> t;
    while (t--) {
        int a, b, c, d;
        cin >> a >> b >> c >> d;
        cout << ((isok(a,b) && isok(c-a,d-b))? "YES\n": "NO\n");
    }
    
    return 0;
}

CF2136B. Like the Bitset

题意

构造一个排列，满足对于若干个点（$s_i=1$），包含该点的所有长度大于 $k$ 的区间最大值都不是该点。

首先，如果有 $k$ 个连续的 $1$ 肯定不行。因为这个区间中总有最大的。

如果没有呢？这意味着每个长度至少为 $k$ 的区间至少包含一个 $0$，贪心地令所有 $s_i=0$ 上的数都比 $s_i=1$ 上的大即可。

AC Code

#include <bits/stdc++.h>
using namespace std;

const int maxn=2e5+100;
char s[maxn];

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    
    int t;
    cin >> t;
    while (t--) {
        int n, k;
        cin >> n >> k >> (s+1);
        
        int len1=0;
        bool ok=true;
        for (int i=1; i<=n; i++) {
            s[i] -= '0';  // important
                    
            if (s[i]) { len1++; }
            else { len1 = 0; }
            if (len1 >= k) {
                ok = false;
            }
        }
        
        cout << (ok? "YES\n": "NO\n");
        if (!ok) {
            continue;
        }
        
        int p0=n, p1=1;
        for (int i=1; i<=n; i++) {
            if (s[i]) {
                cout << p1 << ' ';
                p1++;
            } else {
                cout << p0 << ' ';
                p0--;
            }
        }
        cout << '\n';
    }
    
    return 0;
}

CF2136C. Against the Difference

题意

求一个序列的最长子序列，使得它可以由若干个形如 “$k$ 个 $k$” 的序列连接而成。

考虑 DP，设 $1 \sim i$ 的答案为 $f(i)$，由单调性有转移方程

$$f(i) = \max\{f(i-1), a_i + f(p_i-1)\}$$

其中 $p_i$ 是最后的使得 $[p(i), i]$ 中有 $i$ 个 $i$ 的位置。

AC Code

#include <bits/stdc++.h>
using namespace std;

const int maxn=2e5+100;

int a[maxn];
vector<int> pos[maxn];
int f[maxn], p[maxn];

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    
    int t;
    cin >> t;
    while (t--) {
        int n;
        cin >> n;
        
        for (int i=1; i<=n; i++) {
            pos[i].clear();
            p[i] = -1;
        }
        
        for (int i=1; i<=n; i++) {
            cin >> a[i];
            pos[a[i]].push_back(i);
        }
        
        for (int v=1; v<=n; v++) {
            for (int i=v-1; i<pos[v].size(); i++) {
//              printf("p[%d]=%d\n", pos[v][i], pos[v][i-v+1]);
                p[pos[v][i]] = pos[v][i-v+1];
            }
        }
        
        for (int i=1; i<=n; i++) {
            f[i] = f[i-1];
            if (p[i] != -1) {
                f[i] = max(f[i], a[i] + f[p[i] - 1]);
            }
//          printf("f[%d]=%d\n", i, f[i]);
        }
        
        cout << f[n] << '\n';
    }
    
    return 0;
}

CF2136D. For the Champion

题意

交互题。平面上玩家起始位置未知，你可以作出不超过 $10$ 次平行于坐标轴的移动，移动后返回玩家和一个给定点集的最小曼哈顿距离。求起始位置。

另外，点集坐标与移动距离均不超过 $10^9$。

为了便于思考，把平面转 $45 \degree$，这样曼哈顿距离就变成了切比雪夫距离。

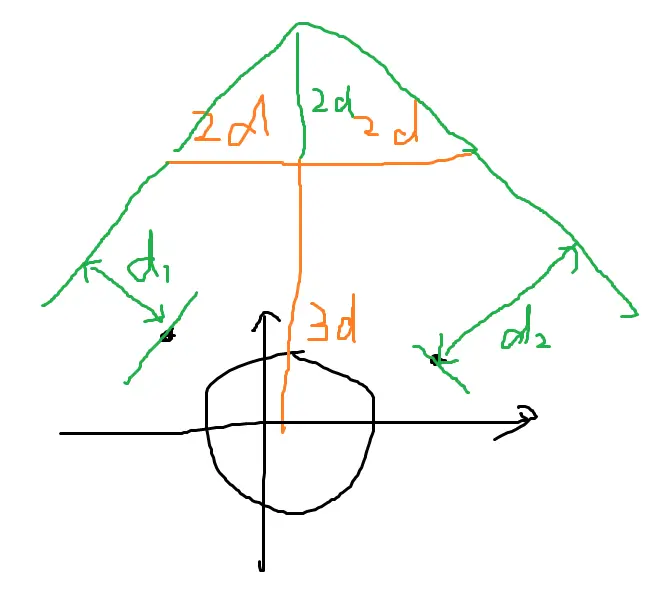
这时发现如果“跳出三界外”，让玩家移出点集的范围，离玩家最近的点就一定是某个坐标最小/大的点（取决于玩家的方向），此时可以直接根据最小切比雪夫距离求出某一个坐标。

具体移动方法如下图橙色部分所示，计算方法如下图绿色部分所示。此时移动 $9$ 次，可以通过。

AC Code

#include <bits/stdc++.h>
using namespace std;

#define int long long
const int d=1000000000;

int move(char dire, int k) {
    printf("? %c %lld\n", dire, k);
    fflush(stdout);
    
    int ans;
    cin >> ans;
    return ans;
}

signed main() {
    int t;
    cin >> t;
    
    while (t--) {
        int n;
        cin >> n;
        
        int mxpy=-2*d, mymx=-2*d;  // max x+y, max y-x
        for (int i=1; i<=n; i++) {
            int x, y;
            cin >> x >> y;
            mxpy = max(mxpy, x+y);
            mymx = max(mymx, y-x);
        }
        
        move('U', d);
        move('U', d);
        move('U', d);
        move('L', d);
        int uymx = mymx + move('L', d);
        move('R', d);
        move('R', d);
        move('R', d);
        int uxpy = mxpy + move('R', d);
        
        int x = (uxpy - uymx) / 2,
            y = (uxpy + uymx) / 2 - 5 * d;
        printf("! %lld %lld\n", x, y);
    }
    
    return 0;
}

CF2136E. By the Assignment

题意

给定一张图，点有点权，图是平衡的当且仅当同起点、终点的每条简单路径的点权异或和都相同。

有些点权未知。问有多少种 $0 \sim V-1$ 的赋值方法使得图是平衡图。

提示：$\oplus$ 有一个很好的性质，就是 $x \oplus x = 0$。

引理

图是平衡图当且仅当所有奇环上的点权为 $0$，且对于所有环，环上的点权都相同。

---

简便起见，定义 $n \otimes x = \displaystyle\bigoplus_{i=1}^{n} x = x(n \bmod 2)$ 以及 $v_S = \displaystyle\bigoplus_{u \in S} v_u$。

必要性：

选择两条 $p \to q$ 的不交的简单路径 $P, Q$，设它们的并为简单环 $R$，则 $v_P \oplus v_Q = v_R \oplus v_p \oplus v_q = 0$。

任选环上另外一个点 $r$，同理 $v_R \oplus v_p \oplus v_r = 0$，于是 $v_q = v_r$。同理，环上任意两点的点权均相同，设相同的权为 $v$。

当 $v \ne 0$ 时，由 $|P| \otimes v = |Q| \otimes v \iff |P| \equiv |Q| \pmod{2}$，有 $|R| \equiv |P|+|Q|-2 \equiv 0 \pmod{2}$。

充分性：

任意选择两条 $p \to q$ 的简单路径 $P, Q$，设它们的并为环 $R$。由于 $R$ 可以分解为若干个有公共点的简单环的并， $R$ 上的所有点权均相同。

1. 若 $R$ 中包含奇简单环，则 $v=0$，命题显然成立。
2. 若 $R$ 中不含奇简单环，则 $R$ 必为偶环

   引理

   对于一个环 $R$，存在若干个简单环 $\{C_i\}$ 使得任意点 $v$ 在 $R$ 中的出现次数等于在 $\{C_i\}$ 中的总出现次数。

   ---

   若 $R$ 非简单环，则存在 $i \ne j, r_i=r_j$。于是可以将该环拆成两个环 $r_i, r_{i+1}, \dots, r_{j-1}$ 和 $r_1, r_2, \dots, r_{i-1}, r_j, r_{j+1}, \dots r_{|R|}$，然后递归拆环。

   由于拆环过程最多持续 $|R|$ 次，且不能拆环时必为简单环（由上可知），即可证明。

   ---

   1. ↩︎
   。于是 $|P| \equiv |Q| \pmod{2} \Longrightarrow |P| \otimes v = |Q| \otimes v$。

这个引理有一个等价的表述：
一个图是平衡图当且仅当边双连通分量内的所有点权相等，且非二分图的边双连通分量点权为 $0$。

具体算法：Tarjan 求边双、黑白染色判断奇环，然后逐个边双判断。

AC Code

#include <bits/stdc++.h>
using namespace std;

#define int long long
const int maxn=2e5+100, mod=998244353;
vector<int> G[maxn];

int V, v[maxn];
int ans;
int dft, dfn[maxn], low[maxn], c[maxn];
bool odd[maxn];
stack<int> s;

void tarjan(int u, int from, int color) {
    dft++;
    dfn[u] = low[u] = dft;
    c[u] = color;
    s.push(u);
    
    for (int v: G[u]) {
        if (v == from) {
            continue;
        }
        
        if (!dfn[v]) {
            tarjan(v, u, !color);
            low[u] = min(low[u], low[v]);
        } else {
            low[u] = min(low[u], dfn[v]);
            if (c[u] == c[v]) {
                odd[v] = true;
            }
        }
    }
    
    // printf("%d: dfn=%d, low=%d\n", u, dfn[u], low[u]);
    
    bool od = false;
    vector<int> co;
    
    if (dfn[u] == low[u]) {
        while (!s.empty()) {
            int v = s.top();
            s.pop();
            co.push_back(v);
            
            if (odd[v]) {
                od = true;
            }
            
            if (u == v) {
                break;
            }
        }
        
        int val = -1;
        for (int u: co) {
            if (val == -1) {
                val = v[u];
                if (od && val>0) {
                    ans = 0;
                    // printf("co of %d let ans=0 (od=%d, val=%d)\n", u, od, val);
                }
            } else if (v[u]!=-1 && val != v[u]) {
                ans = 0;
                // printf("co of %d let ans=0 (od=%d, val=%d|%d)\n", u, od, val, v[u]);
            }
        }
        
        if (!od && val==-1) {
            // printf("co of %d let ans*=V (od=%d, val=%d)\n", u, od, val);
            ans *= V;
            ans %= mod;
        }
    }
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    
    int t;
    cin >> t;
    
    while(t--){
        int n, m;
        cin >> n >> m >> V;
        
        ans = 1; dft = 0;
        while (!s.empty()) { s.pop(); }
        for (int i=1; i<=n; i++) {
            G[i].clear();
            dfn[i] = low[i] = odd[i] = 0;
            c[i] = -1;
            cin >> v[i];
        }
        
        for (int i=1; i<=m; i++){
            int u, v;
            cin >> u >> v;
            G[u].push_back(v);
            G[v].push_back(u);
        }

        tarjan(1, -1, 0);
        cout << ans << '\n';
    }
    
    return 0;
}

CF2136F. From the Unknown (Two Versions)

题意

交互题。有一个宽度为 $w \le n=10^5$ 的编辑器，以如下方式输入单词：

1. 若最后一行可以容纳该单词，则将该单词紧接上一个单词放在最后一行；
2. 否则，新开一行，并将单词置于行首；
3. 特别地，如果词长大于编辑器宽度，编辑器会报错。

你有两次询问，每次给出词长序列，交互器返回最终的行数（若报错则返回 $0$）。你需要求出编辑器的宽度。

在 F2 中，总询问单词数不得超过 $\dfrac{n}{4}$。

F1

首先考虑兜底方案。比如说，打 $m$ 个 $1$。为了唯一区分，我们有

$$\left\lceil \frac{m}{w} \right\rceil < \left\lceil \frac{m}{w-1} \right\rceil \Longleftarrow \frac{m}{w-1} - \frac{m}{w} \ge 1 \iff m \ge w(w-1)$$

可以取 $m = n^2$。

因为有两次询问，可以考虑分块。设块长为 $B$，则 可先询问 $\left( \dfrac{n}{B} \right)^2$ 个 $B$，即可唯一确定每行的块数 $k = \left\lfloor \dfrac{w}{B} \right\rfloor$。

如果 $k=0$，则使用兜底方案。那么如果 $k \ne 0$ 呢？

一个方案是询问 $1, kB, 2, kB, \dots, B-1, kB$。
这是为什么呢？两两一组考虑，当 $i+kB > w$ 的时候，会额外出现一个断行。只需要知道断行的数量就可以反推 $i$ 的值。

F2

我们发现，使用断行方法更优越，若已知 $w \in [L, R] \quad(L \ge 2R)$，则可以用 $2(R-L)$ 个单词求出 $w$。
（注意 $L \ge 2R$ 是必须的，因为这种方法要求编辑器不能报错）

因此，第一次询问不需要唯一确定一块。于是考虑把定长分块和整除分块结合起来，做一个自适应分块。

沿用之前的字母，设第一次询问 $m$ 个 $B$ 得到答案 $a$，且 $w \in [kB, (k+1)B)$。

询问的结果可以推出区间

$$\begin{align*} \left\lceil \frac{m}{k} \right\rceil = a &\iff a-1 < \frac{m}{k} \le a \\ &\iff \frac{m}{a} \le k < \frac{m}{a-1} \\ &\iff \left\lceil \frac{m}{a} \right\rceil \le k \le \left\lceil \frac{m}{a-1} \right\rceil - 1 \\ &\iff w \in \left[ B\left\lceil \frac{m}{a} \right\rceil, B \left\lceil \frac{m}{a-1} \right\rceil \right) \end{align*}$$

注

$a=0$ 不在此列；
对于 $a-1=0$，区间变为 $\left[ B\left\lceil \dfrac{m}{a} \right\rceil, +\infty \right) \cap [1,n] = \left[ B\left\lceil \dfrac{m}{a} \right\rceil, n \right]$，不过之后我们用不到这一点。

若区间能使用使用断行法则使用。这依赖于引理

引理

$$2\left\lceil\frac{n}{a}\right\rceil \ge \left\lceil\frac{n}{a-1}\right\rceil \iff a \ge 2$$

---

必要性 除数不能为零。

充分性：

设 $k=\left\lceil\dfrac{n}{a}\right\rceil$，于是 $a(k-1) < n \le ak$，

而由于 $k \in \mathbb{Z}, k \ge \dfrac{k}{a-1}$，有 $k \ge \left\lceil\dfrac{k}{a-1}\right\rceil$，于是

$$2k \ge k + \left\lceil\frac{k}{a-1}\right\rceil = \left\lceil\frac{ak}{a-1}\right\rceil \ge \left\lceil\frac{n}{a-1}\right\rceil$$

因此对于 $a \ge 2$ 都能使用断行方法。

一个块长调一天

注意

块长很玄学，并且题目给定解很紧，无法放缩，基本无法使用数学方式推导。以下推导仅使用 $2.7 \times 10^4$。

第二次询问的单词数为 $2\left( \min\left\{ n, B \left\lceil \dfrac{m}{a-1} \right\rceil \right\} - B \left\lceil \dfrac{m}{a} \right\rceil \right) \le \min\left\{ 2\left(n-\dfrac{mB}{a}\right), 2B \left( \dfrac{m}{a^2} + 1 \right) \right\}$。

如果 $a$ 过小，则单词数爆炸，不可接受。

设最小的非零 $a$ 为 $A = \left\lceil \dfrac{m}{\lfloor n/B \rfloor} \right\rceil \ge \dfrac{mB}{n}$，有

$$2B \left( \dfrac{m}{a^2} + 1 \right) \le 2B \left( \dfrac{mn^2}{m^2B^2} + 1 \right) = \dfrac{2n^2}{mB} + 2B$$

$a=0$ 时只能使用兜底方案，单词数为 $B^2$。

于是最坏的单词数满足

$$\begin{align*} \text{worst \#words} \le m + \max\left\{\frac{2n^2}{mB}+2B, B^2\right\} \end{align*}$$

当 $B$ 很大的时候，$B^2$ 也会很大，因此我们可以忽略 $2B$ 项。令 $\dfrac{2n^2}{mB} = B^2$，则 $mB^3 = 2n^2$，

$$\begin{align*} m + B^2 &= m + \frac{3}{2} \cdot \frac{2}{3} B^2 \\ &\ge \left( m \left(\frac{2}{3} B^2\right)^{3/2} \right)^{\frac{1}{1+3/2}} \\ &= \frac{2}{3^{3/5}} n^{4/5} \approx 1.03 \times n^{4/5} \end{align*}$$

当 $m = \dfrac{2}{3} B^2$，即 $B = \sqrt[5]{3n^2}, m = \dfrac{2}{3^{3/5}} n^{4/5}$ 时取等。

令 $B=125, m=10400$，则询问的总单词数不超过 $26035$。

只能写程序找最优块长。令 $B=114, m=10655$ 恰好能过^[1]。别问，玄学。

AC Code

#include <bits/stdc++.h>
using namespace std;

const int n=100000, B=114, m=10655;

inline int ask(int r, int b) {
    printf("? %d ", r);
    for (int i=1; i<=r; i++) {
        printf("%d ", b);
    }
    puts("");
    fflush(stdout);
    
    int a;
    cin >> a;
    return a;
}

inline int locate(int l, int r) {
    printf("? %d ", 2 * (r-l));
    for (int i=1; i<=r-l; i++) {
        printf("%d %d ", l, i);
    }
    puts("");
    fflush(stdout);
    
    int a;
    cin >> a;
    
    return r - (a-(r-l));
}

inline int ceildiv(int d, int r) {
    return (d + r - 1) / r;
}

signed main() {
    int t;
    cin >> t;
    
    while (t--) {
        int ans;
        
        int a = ask(m, B);
        if (a == 0) {
            ans = ceildiv(B*B, ask(B*B, 1));
        } else {
            int l = B * ceildiv(m, a),
                r = (a==1)? n: B * ceildiv(m, a-1) - 1;
            r = min(r, n);
//            printf("range is [%d,%d]\n", l, r);
            ans = locate(l, r);
        }
        
        printf("! %d\n", ans);
    }
    
    return 0;
}

---

1. XP3301_Pipi CF 杂题乱做 #1 ↩︎