外观
CF2151
A. Incremental Subarray
题意
求 [1, 1,2, 1,2,3, 1,2,3,4, …, 1,2,3,…,n] 的指定子串的数量,保证答案至少为 1。
答案至少为 1 省了很多事。过于简单,详见代码,不再赘述。
Code
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int t;
cin >> t;
while (t--) {
int n, m;
cin >> n >> m;
bool one=false;
int pre=-1, mx=-1;
for (int i=1; i<=m; i++) {
int a;
cin >> a;
mx = max(mx, a);
one |= (i>1 && a-pre!=1);
pre = a;
}
cout << (one? 1: n-mx+1) << '\n';
}
return 0;
}B. Incremental Path
题意
有一个包含黑白格的长条,初始时有 m 个黑格。一个人有两种操作:
- A:跳到下一格
- B:跳到下一个白格
有一条长度为 n 的操作串 s。一个人将行动 n 次,第 i 次将从 1 出发,依次执行操作 1∼i,并把终点格变为黑色。
求结束后所有的黑色格。
显然第 i+1 次行动和第 i 次行动的前 i−1 次操作是完全相同的。而第 i 次操作可能会因为格子黑白的改变而产生不一样的结果。
于是考虑记录下 i−1 次操作后到达的格子,然后暴力完成剩下两次操作,得到第 i+1 次行动的终点。
由于此算法中一个黑色格子最多被访问 2 次,复杂度是正确的。
Code
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
set<int> black;
char cmd[maxn];
inline int walk(int pos, int ci) {
if (cmd[ci] == 'A') {
return pos+1;
}
do {
pos++;
} while (black.count(pos));
return pos;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int t;
cin >> t;
while (t--) {
black.clear();
int n, m;
cin >> n >> m >> (cmd+1);
for (int i=1; i<=m; i++) {
int a;
cin >> a;
black.insert(a);
}
black.insert(walk(1, 1));
int pre = 1;
for (int i=2; i<=n; i++) {
pre = walk(pre, i-1);
black.insert(walk(pre, i));
}
cout << black.size() << '\n';
for (int i: black) {
cout << i << ' ';
}
cout << '\n';
}
return 0;
}C. Incremental Stay
题意
数轴上有 2n 个点 {ai},要把它们两两配对成 n 条线段。
若一个点最多被 k 条线段覆盖,对于所有 k∈[1,n] 求最大的线段总长。
老办法,考虑把左右贡献拆开,则有
ans=i=1∑nri−li=(i=1∑nri)−(i=1∑nli)=S−2(i=1∑nli)
即最小化左端点的坐标之和。
接下来考虑 k 的限制。等价地,任意前缀点集中左端点数减右端点数不超过 k。
容易想到贪心策略 k 个 LLLL⋯L n−k 个 RLRLRL⋯RL,可以使用逐步调整法证明。每次将 L 往前调,直到不可再调整时即为此形态。
如何计算答案?容易想到前缀和化,设 si=1≤j≤i∑aj,ti=1≤j≤i∑j≡i(mod2)aj,则
i=1∑nli=sk+t2n−k−tk
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=4e5+10;
int a[maxn], s[maxn], t[maxn];
signed main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
for (int i=1; i<=2*n; i++) {
cin >> a[i];
s[i] = s[i-1] + a[i];
if (i > 1) {
t[i] = t[i-2] + a[i];
}
}
for (int k=1; k<=n; k++) {
cout << s[2*n] - 2*(s[k]+t[2*n-k]-t[k]) << ' ';
}
cout << '\n';
}
return 0;
}D. Grid Counting
题意
有一个大小为 n×n 的网格,每个格子有一个黑白的颜色。格子的颜色必须满足:
对于 0≤d<n 恰有一个黑色格子和左上角的切比雪夫距离为 d;
对于 0≤d<n 恰有一个黑色格子和右上角的切比雪夫距离为 d;
第 i 行恰有 ai 个黑色格子。
求着色方案数 mod998244353。
这种“某集合内恰有一个”的思路和数独十分相似,都是先找出可以确定的格子,然后借以排除一系列的格子。如下图,绿色部分代表第 i 步确定的格子(范围),红色部分代表第 i 步排除的格子:
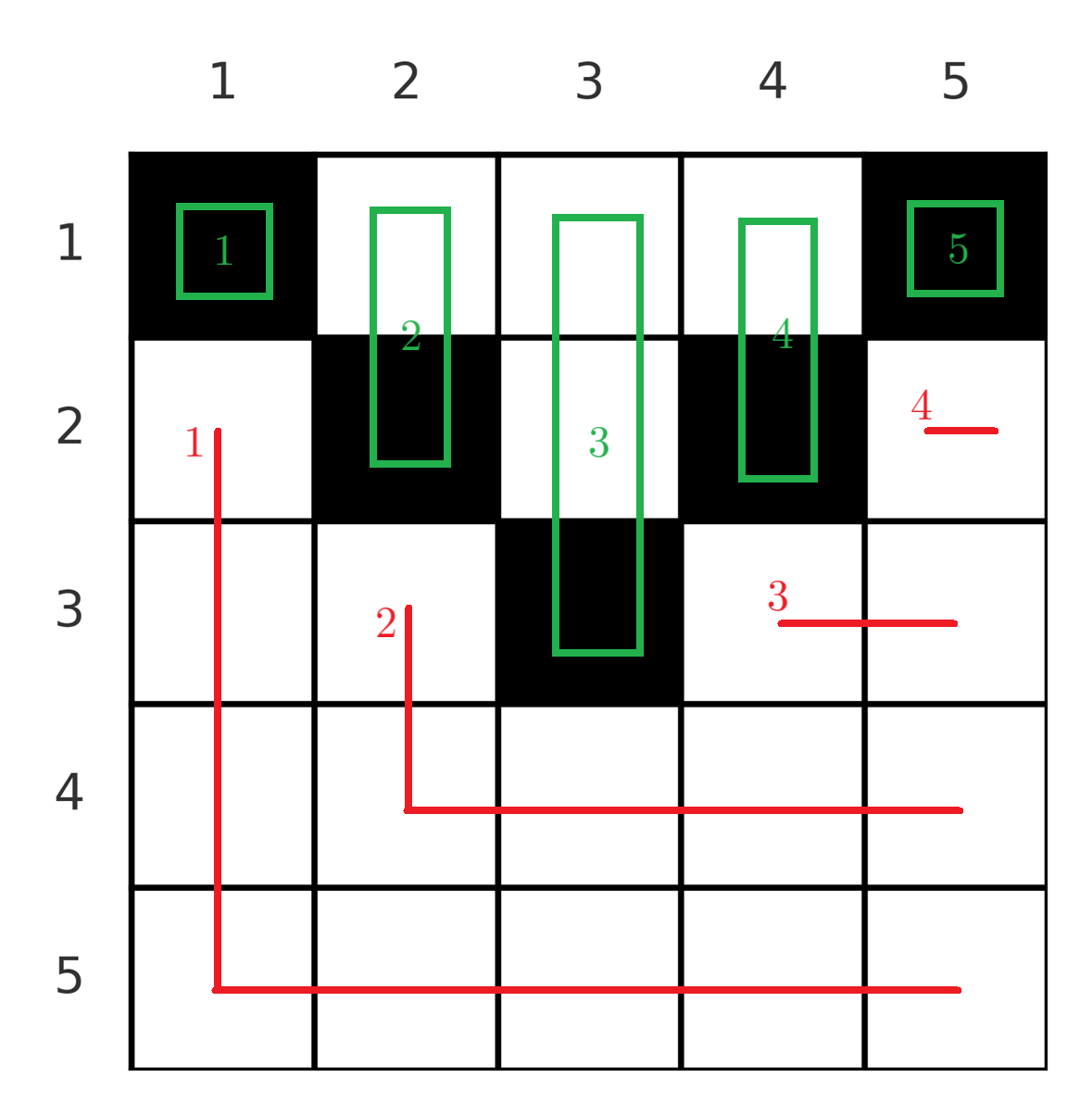
因此,可以证明格子颜色分布满足后两条要求,当且仅当每个绿色区域中恰有一个黑色格子。
考虑从下到上安排黑色格子。设安排到第 i 行之前已经安排了 c 个,则第 i 行有 (aimax{n+2−2i−c,0}) 种安排方式。故
ans=⎩⎨⎧i=1∏n(aimax{n+2−2i−∑j=i+1naj,0}),0,i=1∑nai=notherwise
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=2e5+10, mod=998244353;
int a[maxn];
int fac[maxn], ifac[maxn];
inline int qpow(int x, int y) {
int ans = 1;
while (y) {
if (y & 1) {
ans = ans * x % mod;
}
y >>= 1;
x = x * x % mod;
}
return ans;
}
void pre(int n) {
fac[0] = 1;
for (int i=1; i<=n; i++) {
fac[i] = fac[i-1] * i % mod;
}
ifac[n] = qpow(fac[n], mod-2);
for (int i=n; i>=1; i--) {
ifac[i-1] = ifac[i] * i % mod;
}
}
inline int binom(int x, int y) {
if (x < 0 || y < 0 || x < y) {
return 0;
}
return ifac[y]*ifac[x-y]%mod * fac[x] % mod;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i=1; i<=n; i++) {
cin >> a[i];
}
pre(n);
int ans = 1, c = 0;
for (int i=n; i>=1; i--) {
// printf("ans *= binom(%lld, %lld)\n", n+2-2*i-c, a[i]);
ans = ans * binom(max(n+2-2*i-c,0ll), a[i]) % mod;
c += a[i];
}
if (c != n) {
ans = 0;
}
cout << ans << '\n';
}
return 0;
}E. Limited Edition Shop
题意
有 n 个物品,价值分别为 {vi}。有两个排列 {ai},{bi}。A 和 B 合作,进行游戏。
每回合有两种操作:
- A 取走排列 {ai} 中最早的未被取到的物品;
- B 取走排列 {bi} 中最早的未被取到的物品。
问 A 取走的物品的最大可能总价值。
设 a1,…,ai 和 b1,…bj 都被取走(不管是谁取的)的最大总价值为 f(i,j),
设 {bi} 的逆排列为 bi′,则有状态转移方程
f(i,j)=max{f(i−1,j)+[bai′>j]vaif(i,j−1)(A 尝试取)(B 取)
根据单调性有
f(i,j)={f(i−1,j)+vai,max{f(i−1,j),f(i,bai′−1)},j<bi′j≥bi′
考虑把 j 一维用数据结构维护,根据状态转移方程需要支持区间加、区间推平、单点查询和线段树上二分操作。
时间复杂度 O(nlogn)。
注意
- DP 应有 0 下标,代表未选;
- 由于加完之后线段树内部的单调性可能被打破,因此必须在加之前二分好。
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 2e5+10;
int n;
int v[maxn], a[maxn], ib[maxn];
struct sgt {
int z[maxn*4]; // filled=1 or 叶节点:推平值;否则:增加值
bool filled[maxn*4]; // filled=1 时,等效于下传前先推平
int l[maxn*4], r[maxn*4]; // 在且仅在升序时代表值域
inline int lc(int x) { return x<<1; }
inline int rc(int x) { return (x<<1)|1; }
inline int md(int x, int y) { return (x+y)>>1; }
void pushup(int tn) {
l[tn] = l[lc(tn)];
r[tn] = r[rc(tn)];
}
void pushdown(int tn) {
// printf("pushdown(#%lld, filled=%d, z=%lld)\n", tn, filled[tn], z[tn]);
int lcn=lc(tn), rcn=rc(tn);
if (filled[tn]) {
filled[lcn] = filled[rcn] = true;
z[lcn] = l[lcn] = r[lcn] = 0;
z[rcn] = l[rcn] = r[rcn] = 0;
}
z[lcn] += z[tn]; l[lcn] += z[tn]; r[lcn] += z[tn];
z[rcn] += z[tn]; l[rcn] += z[tn]; r[rcn] += z[tn];
z[tn] = filled[tn] = 0;
}
void add(int tn, int tl, int tr, int x, int y, int a) {
// printf("add(#%lld[%lld,%lld]; [%lld,%lld]; %lld)\n", tn, tl, tr, x, y, a);
if (y < tl || tr < x) {
return;
}
if (x <= tl && tr <= y) {
z[tn] += a;
l[tn] += a;
r[tn] += a;
return;
}
pushdown(tn);
int mid = md(tl, tr);
add(lc(tn), tl, mid, x, y, a);
add(rc(tn), mid+1, tr, x, y, a);
pushup(tn);
}
void fill(int tn, int tl, int tr, int x, int y, int m) {
// printf("fill(#%lld[%lld,%lld]; [%lld,%lld]; %lld)\n", tn, tl, tr, x, y, m);
if (y < tl || tr < x) {
return;
}
if (x <= tl && tr <= y) {
z[tn] = l[tn] = r[tn] = m;
filled[tn] = 1;
return;
}
pushdown(tn);
int mid = md(tl, tr);
fill(lc(tn), tl, mid, x, y, m);
fill(rc(tn), mid+1, tr, x, y, m);
pushup(tn);
}
int query(int tn, int tl, int tr, int x) {
if (tl == tr) {
return z[tn];
}
pushdown(tn);
int mid = md(tl, tr);
if (x <= mid) {
return query(lc(tn), tl, mid, x);
} else {
return query(rc(tn), mid+1, tr, x);
}
}
int max_below(int tn, int tl, int tr, int m) {
// 仅在有序时可用
if (l[tn] >= m) {
return -1;
}
if (r[tn] <= m) { // 等号随意
return tr;
}
pushdown(tn);
int mid = md(tl, tr);
return max(
max_below(lc(tn), tl, mid, m),
max_below(rc(tn), mid+1, tr, m)
);
}
void modify(int i, int a) {
int val = query(1, 0, n, i-1) + a,
pos = max_below(1, 0, n, val);
// printf("max below %lld -> %lld\n", val, pos);
add(1, 0, n, 0, i-1, a);
fill(1, 0, n, i, pos, val);
}
void clear() {
filled[1] = true;
z[1] = l[1] = r[1] = 0; // 清空要完全
}
} segtree;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
// cin >> n;
// while (true) {
// char op; cin >> op;
// if (op == 'a') {
// int i, a; cin >> i >> a;
// segtree.modify(i, a);
// }
// // else if (op == 'q')
// {
// for (int i=0; i<=n; i++) { cout << segtree.query(1,0,n,i) << ' '; }
// cout << endl;
// }
// }
int t;
cin >> t;
while (t--) {
segtree.clear();
cin >> n;
for (int i=1; i<=n; i++) {
cin >> v[i];
}
for (int i=1; i<=n; i++) {
cin >> a[i];
}
for (int i=1; i<=n; i++) {
int b;
cin >> b;
ib[b] = i;
}
for (int i=1; i<=n; i++) {
segtree.modify(ib[a[i]], v[a[i]]);
// printf("modify(%lld, %lld)\n", ib[a[i]], v[a[i]]);
// printf("[ ");
// for (int j=0; j<=n; j++) { printf("%lld ", segtree.query(1,0,n,j)); }
// printf("]\n");
}
cout << segtree.query(1, 0, n, n) << '\n';
}
return 0;
}写这个超融合线段树真是累人。
F. Attraction Theory
题意
数轴上 1∼n 的每个整数位置有一个点,并且每个位置有权值 ai。
每次可以选定一个位置,将这个位置左边的点右移一格,右边的点左移一格。
对于一个可能的状态,设第 i 个点移到了 pi,设所有 {pi} 组成的数列集为 P,求
{pi}∈P∑i=1∑napi
不难发现 {pi} 一定单调,故计数时可以等价为多重集。
设其对应的桶为 {cp},所有桶组成的集合为 C。
对求和换序,则有
ans={cp}∈C∑p=1∑napcp=p=1∑n{cp}∈C∑apcp
接下来我们探究一下 {cp} 可能满足的性质。
引理
{cp} 是满足以下要求的所有数列:
- p=1∑ncp=n;
- 设 l 是 {cp} 的第一个非零项,设 r 是 {cp} 的最后一个非零项,则
- cl,cr∈N∗;
- ∀l<p<r,cp∈{2n+1∣n∈N}。
注意到操作可以任意平移 {cp},因此可以只看非零段,而零的位置不重要。
在平移意义下,操作可以分解为 2 种:
- 把任意三项合并成一项
- 把边界的两项合并成一项
必要性
显然和不变。
而若在中间的三项都是奇数,三项相加仍为奇数。因为初始状态下中间项都为奇数,所以所有合法状态下所有中间项都为奇数。
充分性
考虑对操作进行反向。对于中间的非 1 奇数 c,可以变为 1,c−2,1;对于两端的 c 可以变为 1,c 或 c,1。
容易发现符合条件的非全 1 数列一定能被反向操作,且反向操作后仍然符合条件。因此,所有符合条件的数列都能被反向操作回初始状态。
设所有非零段处于 [l,r] 的合法 {cp} 的集合为 C[l,r],设 s[l,r](i)={cp}∈C[l,r]∑cp,由对称性设
s[l,r](i)=⎩⎨⎧A(r−l+1),A(r−l+1)+b(r−l+1),0,i∈{l,r}l≤i≤rotherwise
于是
p=1∑n{cp}∈C∑apcp=p=1∑n1≤l≤r≤n∑aps[l,r](p)=1≤len≤n∑p=1∑napA(len)#{l∣1≤l≤n,1≤l+len−1≤n}+apB(len)([p+len−1≤n]+[p−len+1≥1])=1≤len≤n∑+ A(len)i=1∑u(len)−1iai+i=1∑u(len)−1ian−i+1+p=u∑n−u+2apB(len)p=1∑nap+p=len∑n−len+1ap=1≤len≤n∑A(len)S(len)+B(len)T(len)
其中 u(len)=max(len,n−len+1)。
S(len) 和 T(len) 都可以用前缀和搞定,接下来看看怎么搞定 A(len),B(len)。
设 W(len) 是方案个数,由和的性质有
2B(len)+lenA(len)=lenW(len)
考虑固定首尾之和为 w,则剩下部分的和为 n−w,对中间各数应用 x↦2x+1,则可以使用插板法,共有
(len−3n−w/2−1)
种方案,则
2B(len)=w∑w(w−1)(len−3n−w/2−1)
W(len)=w∑(w−1)(len−3n−w/2−1)
鸽了。